PROPOSAL
For: linguists, mathematicians, psychologists, pedagogues, teachers, scientists and/or anybody interested in knowing the reason things.
WHAT DO WE HAVE TO THIS DATE?
To this date we have all kinds of dictionaries (language, etimological, ideological, thesaurus, translation ones, …), encyclopedias, we also had resources such as categories, …, taxons, merons, … and lately, covering software like Semantic web, OWL, ... As if we still used Roman numbers. In order to start understanding the power of the Conceptual System, we suggest everybody to read the brief and entertaining texts written by Ferran "Amigo Carles.pdf" (=My friend Carles) (1999) 58 kB, about the anachronism of the alphabetical order system; and also the texts written by Ramon "SistemaConceptualRB.pdf" (=Conceptual System for "non-conceptuals") 367 kB about the exactness of the tree.
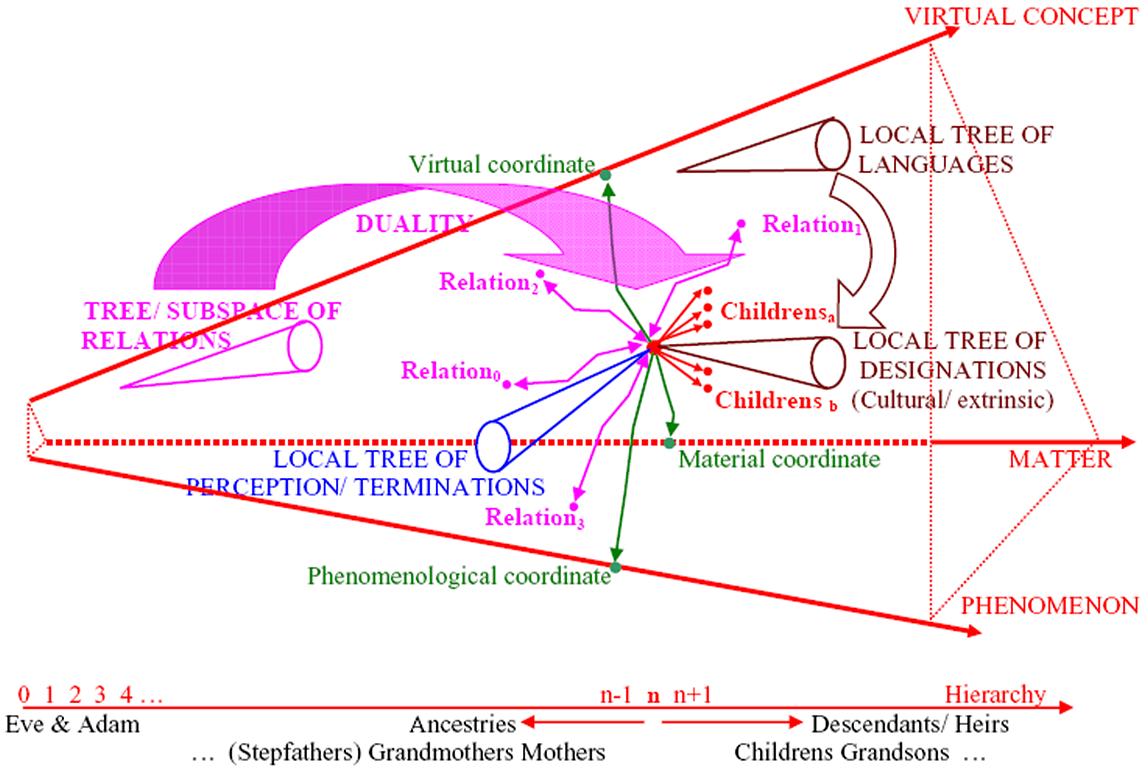
THE CONCEPTUAL SYSTEM
THE TREE
The same tree structure of the indo-arabic numbers, which has brought extraordinary results to the human civilization (as the simple and powerful representation of the enormous quantity 64 785 213),
Ten millions Millions A Hundred thousands Then thousands Thousands Hundreds Tens Units
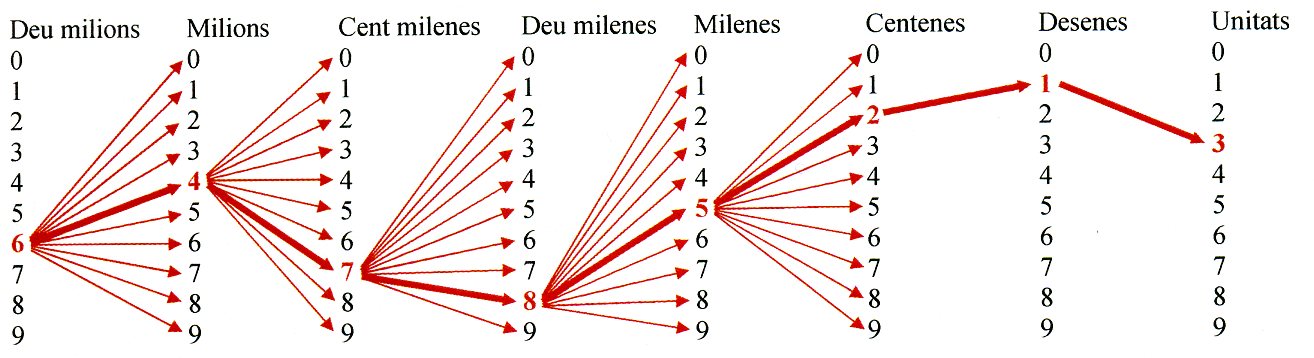
can be used with concepts in general, instead of the present arbitrary criteria, such as the alphabetical or the thesaurus categories.
Because concepts are not by far a set as simple as numbers (these latter ones are characterised by their regular and monotonous sequential nature), the structural methodology has also progressive levels like the numbers (…, thousands, hundreds, tens, units, decimals, …), but its construction criteria (an algebraic algorithm called “(algebraic) Short Exact Sequence” [=“SES”], which the reader doesn’t need to know about) are more complex/ laborious.
PORFIRIUS (s.III) was only a few steps away from finding a system just as exact as the indo-arabic numbers, but of a wider reach, that would have been applicable to all concepts. Despite the progressive and successful implantation of the positional numeric systems during the past 200 years, neither linguists nor mathematicians have taken a step forward so far. They haven’t taken advantage of the “miracle” of the numeric systems*.
* See “KRÖNECKER i el miracle dels sistemes numèrics” (="KRÖNECKER and the miracle of the numeric systems") [.170] in “Conscienciacio” (="Consciousness").
In the numeric systems the partition criterion of the “SES” is fixed, the “equivalence classes modulo 10” (or “equivalence classes modulo 2” in the binary/digital system), which leads to the inductivity which characterizes the numbers (the +1 that we used to study at school). Instead, in the “Conceptual System” the partition criterion is any other concept.
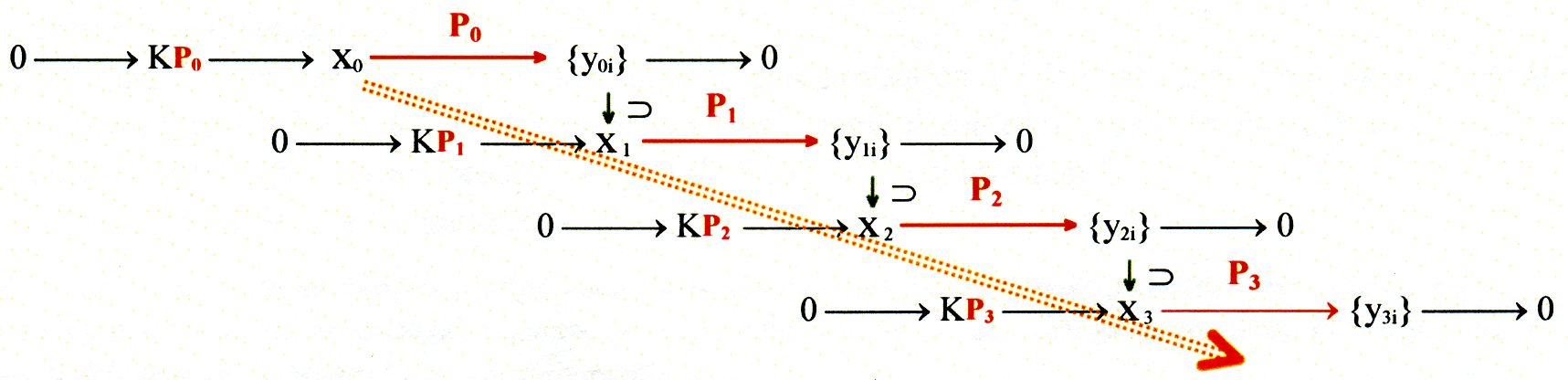
This scheme represents in a mathematical way the construction process. In the SES of the first line, each one of the equivalence classes "y01", "y02", "y03", ... of the set {y0i} generates a new SES which is represented in the following line (x1 € {y0i} if you take into account that they are conceptual contents). Therefore, the red diagonal arrow is one of the many possible lines of descendents generated.
We will call “stepfather” the concept used as partition criterion in every case (the initial concept will be called “mother” and the result are the “children” concepts of the couple. These children form a “family” of more specific concepts).





en spiral, in barred spiral, lenticular, elliptic, irregular, ...;

membranous, fibrillar, globulin, ...;
¿Who would have thought that galaxy, temperament, … or virus generate related “children” concepts? The conceptual system explains exhaustively this ability to establish relationships. And this ability is what allows the transfer in the learning processes, and understanding.
The stepfather provides automatically the distinctive characteristics among the generated children (“Kernel”), that is to say, provides the added abstractions/adjectives, as well as the family characteristics in its own set (“CoKernel”).
CoKernel: The set of all galaxy types, in spiral, disc, lenticular, irregular, … is characterized by its specific shapes.
Even more, there is “polygamy” (something unthinkable in the field of numbers, but necessary in field of concepts, because of their prolific relationships and their “multiple inheritance” characteristic): the same concept, the “mother”, can generate different families with the corresponding “stepfathers” ("a", "b", "c", "d", ...) and different “children”.
b) Mammals [according to their diet] ⇒ Carnivore, herbivore and omnivore mammals
c) Mammals [according to their subClass] ⇒ Prototeris o teris mammals
d) Mammals [according to their Order] ⇒ Monotremas, marsupials, insectivores, ..., Artiodactyla or primate mammals
e) etc., etc., etc.
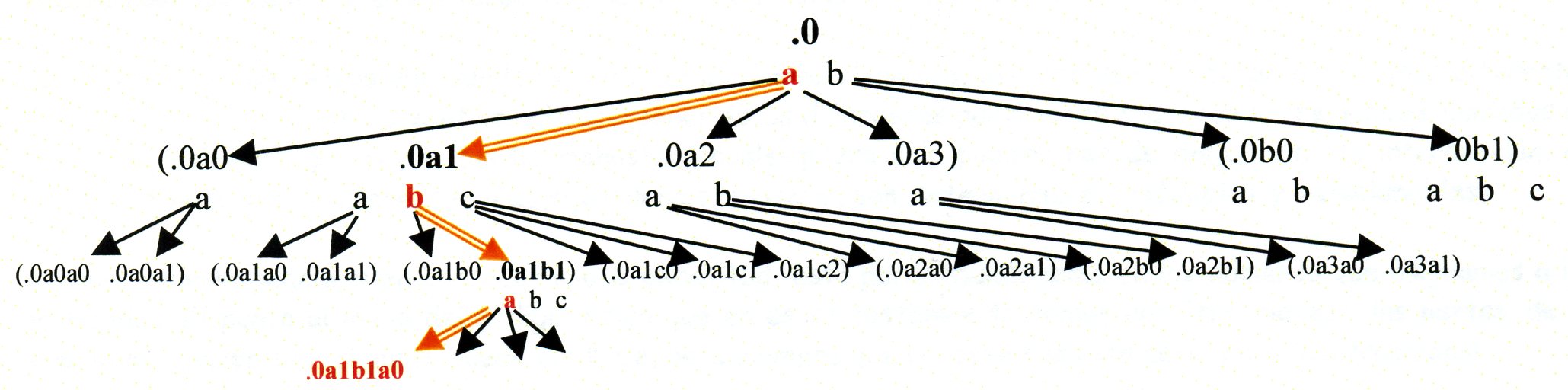
If in the previous scheme only one line of descendants was represented, according to its algebraic process of generation, here, we have the global result: all the lines of descendants, but without these processes. This is the first tree of the “Conceptual System”, the “intrinsic and exact tree of concepts”.
The inductivity and the relationship of multiplicity (10, 2, … according to the basis of the numeric system) of the numbers are replaced in the concepts by the conceptual relationships, linked to the stepfather by the contiguity and the compacity (which originate the corresponding topology).
The “children” are well defined (by the associated mathematical construction), belonging to only one equivalence class.
In each partition there are never any “holes”, that is, there are never any elements the partition of which is unknown or has not been allocated.
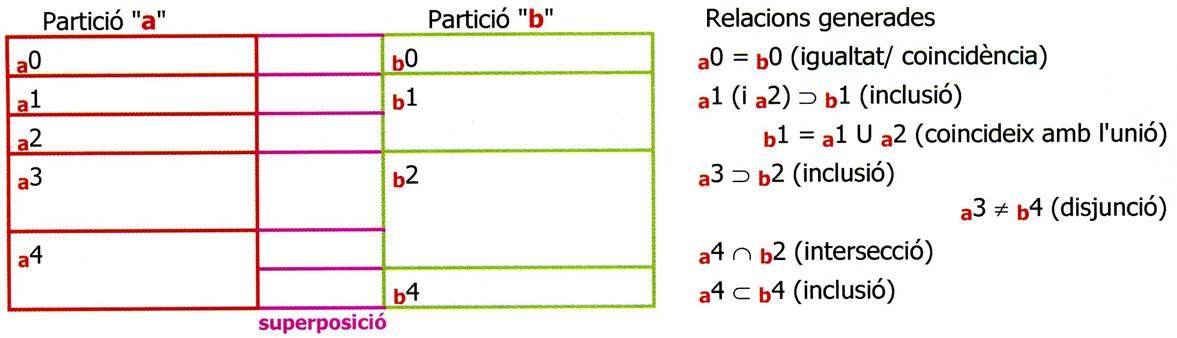
Partició =Partition. Relacions generades =generated relationships. Igualtat/ coincidencia =equality/ coincidence. Inclusió =Inclusion. Coincideix amb l’unio =coincides with the union. Disjunció =disjunction. Intersecció =intersection. Superposició =superposition.
Because of all of this, the intrinsic tree of concepts is more prolific than the tree of numeric systems, and, instead of a surface to represent it (see tree associated with the number 64 785 213), we need a tridimensional espace, as if we were dealing with a real tree.
The important thing is to guarantee the exactness, in this case provided by the corresponding “(algebraic) Short Exact Sequences” [=“SES”]. We cannot do what we think it’s better or easier, as it has been done to this date (as done with encyclopedias, language dictionaries, synonymous dictionaries, with the “Categories”, with the “Taxons”, with the “Ontology”, with the “mental maps”, etc…). The difficulty is double (but at the same time, it has a double use):
THE INTRINSIC PARTITION (The most generic/ universal and intrinsic concepts to our mind)
- Sensitive concepts [Structural level 1]:
- Sensitive static concepts (“Matter”), from the age of one year old and the linguistic signs;
THE RELATIONSHIPS: THE MOST POWERFULL RESOURCES
We already have relationships like the ones already mentioned: hierarchical, stepfather and Boolean relationships. But it is even more important to add the establishment of relationships between any two concepts (the lector must know that from two concepts which are correctly related, a simple knowledge is always generated). This new ability to establish relationships can be applied by using relationships, or even normal concepts duly transformed into relationships via the “Star operator” of the "Algebraic duality".
With these relationships we are superimposing a multicolour web onto the tree of exact concepts. This implies uncountable and perfectly represented pieces of knowledge and, for the same reason, manageable (reusable, easily operated …). As the “Cognitive Space” appears, the learning becomes a simple and gratifying navigation journey.
See "Brief comment" (1999) 85 kB and also "The Wisdom tree.pdf" 221 kB
Each concept becomes a conceptual map, but intrinsic, with all the associated knowledge and the possibility of navigating through the intrinsic relationships that define these pieces of knowledge.
As in any process: the discipline of observing an adequate methodology leads to a useful/ applicable res.
With the conceptual system, such a virtual and mathematically elaborated concept as the “Nilpotent Element”, becomes understandable to almost anybody who is interested. See "Element nilpotent.pdf" (=“Nilpotent element.pdf”).
With the conceptual system it is trivial to differenciate –in order to use them correctly- between concepts such as “Program”, “Project” or “Planning”. See "Programa projecte planificació.pdf" (=“Program project planning.pdf”).
Writing well, understandably and avoiding ambiguous texts, is as easy with the conceptual system as using a spelling correction tool. See "Aplicacions als Hipertextos comprensius i correctors del contingut del text" (="Applications to the hypertexts that understand and correct text content").
With a conceptual System, the translation from/to any language is automatic, because it uses the said system as referencing tool of the text (which only uses as reference the dictionaries of the two languages). "Aplicacions a la Traducció automatica".
Partial wiew to Shappe (=Forma.pdf) relationability
FINAL RELEXION AND EXPECTATIONS
To move from
the current linguístic “system” to the "Conceptual system",
would be similarly to moving from the use of
Roman numbers to the Arabic numbers.
200 years ago, with the “socialization” (global implementation) of the positional numeric systems (decimal, …) nobody could have imagined the spectacular development that they would imply for mathematics, science, technology, economy (globalization), software (binary positional numeric system), … which has been possible due to its exactness and its intuitiveness.
However, at present, we cannot imagine the implications of the extension to all concepts of a similar exact and intuitive (intrinsic) representation. Therefore, it is logical that people are surprised by its possible application to distant areas such as genetics (see "Aplicacions a la bioquímica i la genètica" ="Applications to biochemistry and genetics") or quantum mechanics (see "Aplicacions a la Mecànica quàntica" ="Applications to Quantum Mechanics").
In the first case, it is even common sense: the genetic codification is a structure of systems of the (+M, +S), type, a lot simpler than the ones of the (-M, +S) type of the psyche. Furthermore, the codification of the psyche derive from the genetic codification. Consequently, any structure/ characteristic of the genetic codification is surely present in the psyche. For all of this, the knowledge of psychic codifications can provide information on the genetic codifications.
In the case of quantum mechanics, the complexity and the surprise caused by the phenomena that are being discovered cause every day more questions raised than explanations given: “we need a theory that today we cannot even imagine” (A. J. LEGETT), “The mystery of the origins of the Universe is far from being resolved” (G. SMOOT). This “Unimaginable theory” or “solution to the mystery” could perhaps be provided, thanks to certain pointers, by an informational structure of the (-M, +S).